A Brief Investigation into Passive Solar Home Design in Humboldt County

Bonnie L. Oliver, Architect & Dale R. Oliver, HSU Mathematics

Passive solar homes in the Northern Hemisphere are typically rectangular designs with the long sides running East-West, and with windows primarily on the southern facing side of the house in order to absorb the sun’s heat energy to warm the house during the winter.  In order to stay cool in the summer, many passive solar homes rely on shading (control) to keep the house cool.  The energy required to heat and cool a well-designed passive solar home is usually less than 20% of the energy required for conventional home of similar size.

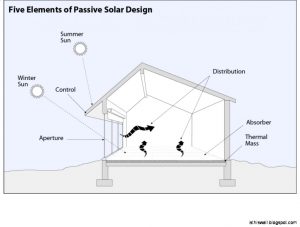
In the coastal areas of Humboldt County, including most towns in and around Eureka, we don’t worry about controlling for summer sun, since the average high temperatures throughout the year are below below that of our interior spaces. For example, the warmest average daily high temperature in Arcata, based on historical data, is 64 degrees Fahrenheit on September 2.  Thus, our goal in this activity is to explore how much window area on the southern-facing side of a house is needed to significantly reduce the energy required for heating, without excessively overheating the house on a day of full sun.

DOWNLOAD THE LESSON HERE

Other resources

1. There is a complete Energy-Efficient Housing Unit at www.teachengineering.org with some interesting hands-on projects, including a zero-energy housing activity.  Check it out!
2. The cost per Million Btus for a high efficiency Heat pump is less than $20.

Some of the relevant standards:

CCSSM

• Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays. (Grades 9 – 12)
• Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters. (Grades 9 – 12)

NGSS

• Evaluate competing design solutions using a systematic process to determine how well they meet the criteria and constraints of the problem. (Grades 6 – 8)
• Evaluate a solution to a complex real-world problem based on prioritized criteria and trade-offs that account for a range of constraints, including cost, safety, reliability, and aesthetics, as well as possible social, cultural, and environmental impacts. (Grades 9 – 12)